ASCII Roguelike Map Generation (Failures)

The first of potentially a lot of gamedev blog posts from me!

So, for a little while now, I’ve had a project on the backburner (currently) titled Ascetic of the Cabal. It’s a 2D roguelike RPG, in the style of classic roguelikes like, uh, Rogue. It’s been something I’ve been plucking away at here in there in my off hours, never to a significant degree of progress, but I’ve recently wanted to spend a bit more time and energy actually getting it into a cool playable game, and with that I’m hoping to have a bit more hands-on gamedev to talk about on here, so I’d like to spend some time chronicling what I’ve been working on lately: map generation.

A High Level Primer

So, the premise of Ascetic is sort of a strange one, a kind of riff on Lovecraftian-style cosmic horror, just dragged a little bit more into the spotlight in a way a bit more aligned with something like a Dishonored.

Ascetic takes place in a sort of alternate-1920sish? America, one where the United States was built on a North American continent that was awash with unknowable, eldritch gods, beings of incomprehensible power and indecypherable motivation which peppered the landscape. Instead of defeating these gods or hiding from them, America was built in partnership with them, with cities canonizing these beings as their patron gods, offering them favor and worship in exchange for their power and protection. Thus, a modern America has been built with these strange beings always in the wings, skyscrapers erected over shrines to Great Old Ones.

The problem is that there wasn’t enough worship to go around when the initial terms of this deal were struck, so some of these gods, the less savory ones, now referred to collectively as The Cabal, got left out to dry: no shrines, no canonization, no state-mandated worship, diddly squat. These gods reside in the shadows, spiteful towards their brethren which got the sweet end of this deal, and their small, devoted, illegal gathering of followers, constantly set out on holy quests to strike down the City Gods as punishment for their betrayal.

This is the general premise of Ascetic of the Cabal. You are one of the followers of this Cabal of forsaken gods, and your mission is to go into a great City, home to 5 City Gods, and in a single life strike them all down, clearing the way for the Cabal to take over. In video game terms, in a single life, you must find and defeat 5 bosses in a procedurally-generated open city, and on death you lose all of your items and progress (generally, more on that another time), the City gets scrambled up and repopulated, and you try again ‘til you do it.

So, that’s the premise, now let’s talk about building that there City.

Disclaimer

The process I am about to describe is, at least I think for the goals of this development, wrong. This was my first pass at these mechanics and I think they were the wrong one. However, I think chronicling what I did, why it’s wrong, and what I have learned and what to do instead, I think is interesting. Where a particular thing I did is particularly wrong in some way, I’ll leave a footnote.

The Goals of Map Development

So, my goal with map generation (henceforth I’m gonna refer to all of the playable game-space as the “map”) was to create something suitably approximating a mid-sized American city, populated with a street grid, buildings, residents, and the other ephemera of a city (like, I dunno, fountains and benches and stuff).

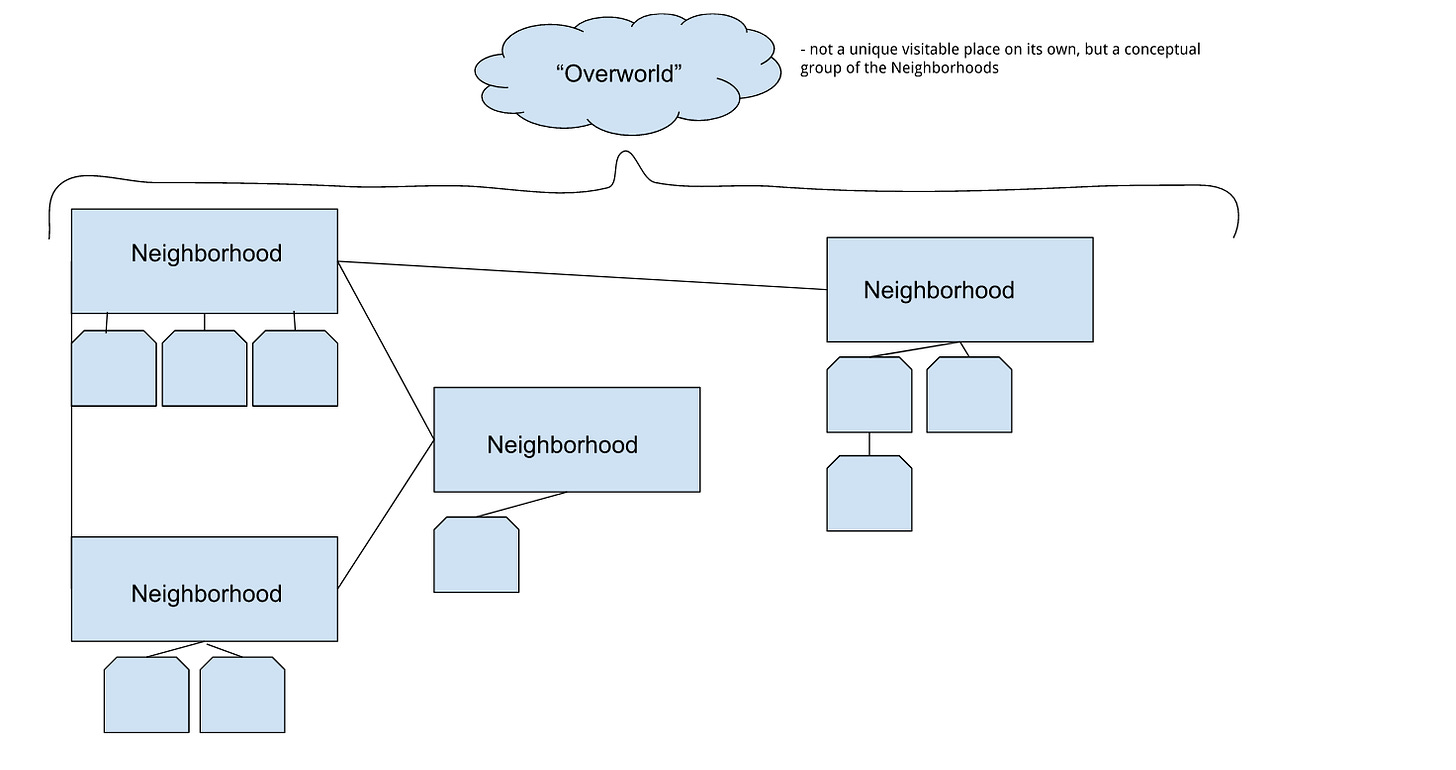
Rather than just generating a single colossal map that the entire game takes place in, it seemed beneficial to chunk the map into subsections I’ve taken to referring to as Neighborhoods. I figure this division has benefits in multiple dimensions of the design:

1. It serves as a solid logical division of the game space. I can assign a single God to a single Neighborhood, and have that be its “domain”. In doing so, I can seed the random generation of that Neighborhood in such a way that it feels of the associated God (as an example, if a God of Drunken Revelry is based out of a certain Neighborhood, I can tip the scales on the procedural generation to populate that neighborhood with more bars, drug dealers, drunk people, and booze)

2. It makes things more convenient from a programmatic sense. I only need to have a single Neighborhood loaded at a time, and thus only needed to keep track of the contents of one part of the city at a time, rather than the entire city. This means I only have to keep track of 1/Nth of AI-controlled characters, only need to render 1/Nth of the map, etc, where N is the number of Neighborhoods (assuming approximately equal distribution of game elements across the Neighborhood).

As far as the division of the game world goes, it’d look something like this:

Each Neighborhood is a separate space in the game, connected to each other by loads. The net sum of them logically forms the “overworld” of the game, although such a space does not exist independent of the constituent Neighborhoods. Each Neighborhood also contains an arbitrary number of buildings which are also independent spaces from the Neighborhood in which they exist, connected by a load.

So, that was the goal, so here was the methodology I set out it with filling out:

1. Generate a single, “overworld” land mass randomly. This mass needed to be a single, contiguous piece of game map (2D, luckily) that I could split up for later

2. Divide this single chunk of landmass into Neighborhoods

3. Earmark points between these Neighborhoods as “gates”, transition points through which the player can move from one Neighborhood to another

Generating The Overworld Mass

The first step was just to create a big-ol blob of land that I could then get to hacking and slashing. Here’s the Python code block. If you can’t read code, or you just don’t want to waste a bunch of time reading a big block of spaghetti, just scroll past it, I’ll walk through it right afterwards.

world_size = game_constants.size_world
ws_percentage = game_constants.world_size_percentage

#1. Instantiate a square world of N x N, where n=size_world
world_map = [[True for x in range(world_size)] for y in range(world_size)]

#2. Create a deletion candidates list of tuples, featuring every edge space (and corners twice)
deletion_candidates = []
for n in range(world_size):
    deletion_candidates.append((n,0))
    deletion_candidates.append((0, n))
    deletion_candidates.append((world_size-1, world_size-1-n))
    deletion_candidates.append((world_size-1-n, world_size-1))
        
#3. Delete spaces by randomly selecting candidates out of deletion_candidates, then enqueuing their neighbors
spaces_to_delete = ceil((world_size * world_size) * (1 - ws_percentage))
for x in range(spaces_to_delete):
    space_selected = choice(deletion_candidates)
    world_map[space_selected[0]][space_selected[1]] = False
    deletion_candidates.remove(space_selected)

    if space_selected[0] > 0 and world_map[space_selected[0]-1][space_selected[1]]:
        deletion_candidates.append((space_selected[0]-1, space_selected[1]))

    if space_selected[0] < world_size-1 and world_map[space_selected[0]+1][space_selected[1]]:
        deletion_candidates.append((space_selected[0]+1, space_selected[1]))

    if space_selected[1] > 0 and world_map[space_selected[0]][space_selected[1]-1]:
        deletion_candidates.append((space_selected[0], space_selected[1]-1))

     if space_selected[1] < world_size-1 and world_map[space_selected[0]][space_selected[1]+1]:
        deletion_candidates.append((space_selected[0], space_selected[1]+1))

Alright, so let’s step through this step by step. First bit’s pretty simple:

world_size = game_constants.size_world
ws_percentage = game_constants.world_size_percentage

#1. Instantiate a square world of N x N, where n=size_world
world_map = [[True for x in range(world_size)] for y in range(world_size)]

game_constants is an external file of random game config data that I’m importing in. world_size is an integer N, such that I want a game map to be generated starting from an NxN square of grid spaces. world_size_percentage is a decimal between 0 and 1 representing how much of that NxN grid I want to survive the approaching roughing-up of this map. It’ll come back into play later.

For now, I start by instantiating world_map, a 2-dimensional matrix of boolean values of size NxN. I just set all of them equal to True, indicating that there is playable game space there.

(As an aside, if you’re unfamiliar with this weird fuckery notation I have going on there, may I introduce you to Python List Comprehensions, an absolutely sexy language feature of Python which lets you generate long lists (or even objects!) of data from simple logical relations. This basically reads as [make a list of world_size [make a list of world_size “True”s]s])

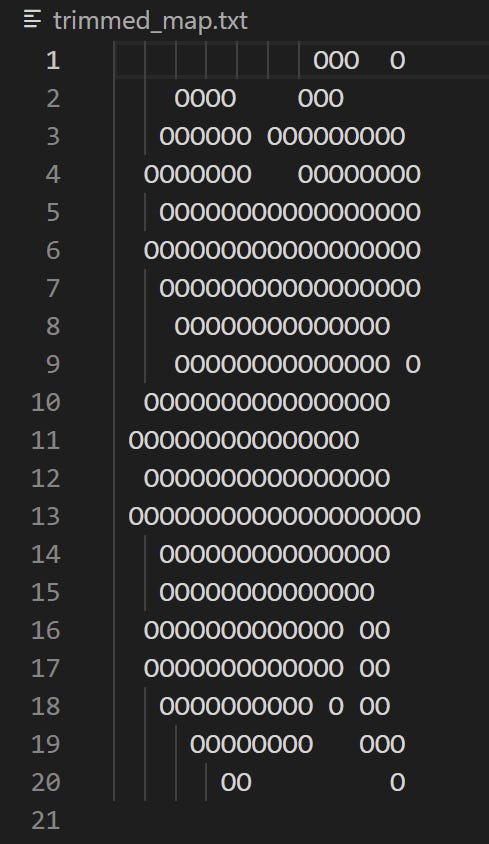
Basically, for a world_size of 20, it generates this, where every O represents a space that currently exists in the game world:

Next up is this bit:

#2. Create a deletion candidates list of tuples, featuring every edge space (and corners twice)
deletion_candidates = []
for n in range(world_size):
    deletion_candidates.append((n,0))
    deletion_candidates.append((0, n))
    deletion_candidates.append((world_size-1, world_size-1-n))
    deletion_candidates.append((world_size-1-n, world_size-1))

So, what I’m doing here is creating a list of deletion candidates, spaces from this big NxN blog of spaces that I want to remove from the shape, thus sort of carving this big square away into, hopefully, a more organic looking shape. I create a list, and using this for-loop, I insert into it every single space on the edge of this square as a starting set.

Eagle-eyed readers (or just those who read the comment), will notice that I’m using a list, which can include the same item multiple times, and not a set, in which every element must be unique from one another, and, as a result of the way I’m initializing this list of candidates, the corners will be included twice. I did this on purpose! I wanted to favor generating a sort of rounded shape and try to reduce the number of bits that spike or jut out of the main blob, so I figured I’d have every single deletion candidate represented S times in the list, where is the number of “exposed” edges it has. As the map gets whittled away at, spaces that get sort of carved around will be more likely to be removed themselves.¹

#3. Delete spaces by randomly selecting candidates out of deletion_candidates, then enqueuing their neighbors
spaces_to_delete = ceil((world_size * world_size) * (1 - ws_percentage))
for x in range(spaces_to_delete):
    space_selected = choice(deletion_candidates)
    world_map[space_selected[0]][space_selected[1]] = False
    deletion_candidates.remove(space_selected)

Now we get chopping! Note that we generate the number of spaces we want to shave off of our square here by just taking the inversion of the world_size_percentage from earlier and multiplying it by the total number of spaces in the grid. If your world_size is 10, you have a 10x10 grid of 100 spaces, then if your world_size_percentage is 0.6, then you want to remove 40% of the spaces, or 40 spaces.

So, spaces_to_delete number of times, we use python’s choice function to randomly select a space from our deletion candidates, mark it as False (indicating that it is no longer playable game space), and removing it from deletion candidates.² Thanks to Python's implementation of choice, this is O(XlogN), where X is the number of deletions we make and N is the size of world_size, so it could be a lot worse, but also not great tbh.

A Brief Lil’ Aside About Big(O)

If you aren’t a programmer, or if you are a programmer but didn’t receive a formal university Comp Sci education (smart!), you might not be familiar with the concept of Big(O) notation.

Basically, in particular when it comes to building algorithms, as I am doing here, building an algorithm of random game map generation, we as programmers have a lot of possible ways of doing things, and the main criterion we generally evaluate these methods with, although far from the only, is how fast our algorithm does the thing we want it to, or more accurately how the speed of our algorithm scales to the size of the problem we give it.

If you’re writing an algorithm to, say, sort a list of numbers, pretty much any solution you come up with will sort a list of 10 numbers nigh-instantly; modern computers are pretty fast, after all. However, when you reach a list of a million numbers, suddenly certain algorithms that scale poorly will take forever, whereas optimized algorithms will only take the absolute minimum amount of time it needs to.

While you can run exact tests of speed and take precise measurements, a lot of it has to do with fiddly bits unrelated to the algorithm itself, like the hardware we’re running on, so as a convention we usually describe an algorithm’s speed scaling factor in a sort of scribbled-on-bar-napkin sort of approximation called big-O, which represents a worst-case runtime.

To wrap your head around it, here some example operations you might do to a list of numbers, and their big-O speeds.

• Grabbing the first number out of a list is O(1), or a constant time operation. No matter how long a list of numbers is, the time it takes to grab the very first one is exactly the same every single time.³

• Finding a given item out of an unsorted list is O(n), or linear time. Worst case scenario, it’s the very last item you check, or it’s not even in the list, and so you have to check every other item in the list once to make sure it’s not the one you are looking for. 100 numbers in the list, worst-case, you gotta check all 100 of them to verify that the item you’re looking for isn’t there

• A lot of really shitty algorithms you could use to sort a list of numbers are O(n^2), or quadratic runtime, or absolute dogass. For instance, many people’s first intuitive idea on how to sort a list is to find the lowest item in the list, move it to the front, then find the second lowest item, move it next, and so on. This algorithm is called “bubble sort”, as the lower items “bubble” up to the top of the list, and it sucks shit on a computer. Consider the worst-case, in which the list is sorted in the exact opposite order you want it sorted (so, high-to-low, in this example). In this case, you need to traverse the entire list to find the next lowest number of the unsorted numbers at the very end of the list, every time. Traversing the entire list of length N for every single placement, for N placements, is N x N or N^2 operations⁴

• Some algorithms run in worst-case O(n!) runtime, or factorial runtime. These algorithms are mostly created by computer scientists as jokes, because we don’t get out a lot. For instance, you have bogosort, a joke sorting algorithm which attempts to sort a list by just randomly shuffling it and seeing if it accidentally sorted it, the programming equivalent of throwing a deck of cards at a wall, picking all of the cards off of the floor, checking to see if you accidentally sorted the deck, and repeating until you have

• Actually, that’s technically not 100% true. Bogosort is only O(n!) if you can’t repeat permutations, as that’s the number of permutations that exist of n elements. If you can repeat permutations, as you hypothetically could if you were truly randomizing them, you might just never sort the thing, no matter how short the list is.

Anyways, yeah, I add all of this just to say that my algorithm’s O(XlogN) runtime is, actually, pretty bad. We’ll get back to that later.

Anyways Back To The Algorithms

 if space_selected[0] > 0 and world_map[space_selected[0]-1][space_selected[1]]:
        deletion_candidates.append((space_selected[0]-1, space_selected[1]))

    if space_selected[0] < world_size-1 and world_map[space_selected[0]+1][space_selected[1]]:
        deletion_candidates.append((space_selected[0]+1, space_selected[1]))

    if space_selected[1] > 0 and world_map[space_selected[0]][space_selected[1]-1]:
        deletion_candidates.append((space_selected[0], space_selected[1]-1))

     if space_selected[1] < world_size-1 and world_map[space_selected[0]][space_selected[1]+1]:
        deletion_candidates.append((space_selected[0], space_selected[1]+1))

Oh god where was I. Right, this last bit of the square-trimming algorithm. Basically, after we have randomly selected a space for removal and removed it, we check all four of that space’s neighboring spaces to see if they A) exist (as they wouldn’t in the case of, say, the top-edge’s northern neighbor) and B) haven’t themselves been deleted yet. For each of those spaces that fits those criterion, they are now definitionally edges themselves and are added to deletion_candidates, potential victims of the following random selections.

So, we make so many random deletions from the edges of the shape until we have reduced the total landmass by the proportion we want. So, for our 20x20 world up there, when I give it a world_size_percentage of 0.6 (that is, I want 40% of it lopped off), it might leave me with something like this:

You can see we sliced up a fair bit of the landmass. The corners have, generally, been rounded away, and it even got in a bit deep there and gouged out some decent little inlets in the top middle and bottom right there. But, we have a couple problems!

Those two little zones there are islands: they’re not connected to the primary landmass, and I don’t want that, I want one big ol’ block of land I can divide later, so we need to get rid of them. This is one of those things that’s really easy for a human being to spot, but kind of a pain in the ass to tell a computer to do, so lemme explain what I do. I’m not going to post the whole code block, but the pseudocode looks like this.

put every space remaining into a big ol' set called unexplored_land
create an empty list of islands, each comprised of size 0 and an empty list of constituent spaces
instantiate largest_island to an empty island of size 0

while there are still spaces in unexplored_land:
    instatiate a new island of size 0 and an empty list of constituent spaces
    instantiate an empty queue of spaces to check
    pick a random-ass point from unexplored_land, put it in the queue
    while there are points in the queue:
        remove a point from the queue
        add it to the new island's consituent spaces
        increment the new island's size by 1
        add all of that point's neighbors that exist and are still in unexplored_land to the queue
    if new island is bigger than largest_island:
        delete all of the spaces in largest_island from the map
        set new island to be the new largest_island
    otherwise:
        delete all of the spaces from the new island from the map

Alright, so what’s going on here. I am essentially identifying islands using an algorithm called breadth-first search on random spaces of land in the map. I pick a random point on the map, then I essentially mark it as “belonging” to a given island, then I take every neighboring space to that one space that I haven’t checked yet and put it into a queue, a sort of “to explore” list. I then repeat the process with every single point in that “to explore” list until I have no more adjacent spaces to explore, having therefore explored all of the spaces contiguous to that first space I grabbed.

I then continue doing this as long as there is any land in the map I haven’t yet explored, keeping track of the largest of these islands I’ve explored. Whenever I finish exploring an island, if it’s the biggest one I’ve found so far, I keep it and destroy the last biggest one. If it isn’t, I destroy this one I just found, and keep looking. At the end, only the biggest island remains on the map. Here’s what that 20x20 looks like after doing this:

See? Those two little islands in the corners have gone the way of Bikini Atoll, having been blasted to shit straight off the map. Now we’re left with one big ol’ continuous landmass, and landmass generation is done.

This whole process isn’t actually that bad, runtime wise. In the worst-case (and in fact in the best-case too), we explore every space on the island precisely once to attribute it to one island or another. O(n), where n is the number of spaces in the map, and I don’t think there’s a way to do it where you don’t have to check every space, so I’m calling that a W.

There Goes The Neighborhood

So that’s a third of the work done, we have a big landmass, now we want to split it into Neighborhoods: discrete, continuous subsections of the map. How the hell do we do that?

Welp, here’s what I wrote. As before, lemme give you the whole code block, then I’ll walk through it step-by-step.

#1. Generate N random "home" points for N neighborhoods
num_neighborhoods = game_constants.number_of_neighborhoods
world_size = game_constants.size_world
neighborhood_cores = []

while len(neighborhood_cores) < num_neighborhoods:
    candidate = (randrange(0, world_size),randrange(0, world_size))
    if world_map[candidate[0]][candidate[1]]:
        conflicting_cores = [core for core in neighborhood_cores if dist(core, candidate) <= 4]
        if not conflicting_cores:
            neighborhood_cores.append(candidate)

#2. Create N sets which will contain the points located in each neighborhood
neighborhoods = [{"core": core, "points": [], "gates": []} for core in neighborhood_cores]

#3. Calculate the closest core to each space on the world map, and assign that point to the neighborhood associated with that point
for x in range(world_size):
    for y in range(world_size):
        if world_map[x][y]:
            closest_core = -1
            closest_core_distance = 100000000
            for n in range(num_neighborhoods):
                core_distance = dist((x,y), neighborhoods[n]["core"])
                if core_distance < closest_core_distance:
                    closest_core = n
                    closest_core_distance = core_distance
                    neighborhoods[closest_core]["points"].append((x,y))

Alright, so, what the fuck is this doing? Let’s find out.

#1. Generate N random "home" points for N neighborhoods
num_neighborhoods = game_constants.number_of_neighborhoods
world_size = game_constants.size_world
neighborhood_cores = []

This is some easy-peasy instantiation. We’re grabbing the number of neighborhoods we want to make from the game config, as well as the size N of the world (this code lives in a different function than the previous block, so we need to either do this, or save this value in the parent class, which, eh, feels redundant). We’re also instantiating a list called neighborhood_cores, what this is eventually going to do is hold a series of coordinates which will serve as the anchoring points for each of our neighborhoods.

while len(neighborhood_cores) < num_neighborhoods:
    candidate = (randrange(0, world_size),randrange(0, world_size))
    if world_map[candidate[0]][candidate[1]]:
        conflicting_cores = [core for core in neighborhood_cores if dist(core, candidate) <= 4]
        if not conflicting_cores:
            neighborhood_cores.append(candidate)

Now, this block of code is responsible for creating those anchoring points, and it definitely needs some work, but let’s take a look at what it does do.

So, the while loop basically ensures this process will repeat until we have a core for every single neighborhood. The process itself constitutes taking a random point from somewhere in the world map, and then checking if that point is usable game space (checking if it’s an “O” on one of the printouts I’ve been showing you, essentially). Then, it compares that point to all of the other points it’s already canonized as neighborhood cores, making sure it isn’t too close to any of them.

In this case, I’m using a hard-coded value of 4 for comparison. What I should do instead is use a value set in the config like all of the other values I’ve been pulling, like world_size, or even better, it should probably be cleverly derived from the world size in order to always be appropriately scaled to the world size, whatever it may be, but that requires tweaking to figure out the secret sauce for what that proportion should be and I’m too lazy to do that right now while I’m still prototyping, so hardcoded value it is.

Anyways, yeah, if the point we’ve sampled exists in the game map and is suitably far from every other core we’ve chosen, then the point is chosen as a core, and we repeat, until every neighborhood has a point to serve as its core.

#2. Create N sets which will contain the points located in each neighborhood
neighborhoods = [{"core": core, "points": [], "gates": []} for core in neighborhood_cores]

This is the instantiation of a data structure which will represent every neighborhood we create. It’s a list of neighborhood objects, each containing a core tuple, one of the points we just sampled above, a list of all of the points comprising the neighborhood (this will eventually also include the core, but doesn’t at init, we’ll get to that in a sec), and gates, which we’ll get back to in a sec.

#3. Calculate the closest core to each space on the world map, and assign that point to the neighborhood associated with that point
for x in range(world_size):
    for y in range(world_size):
        if world_map[x][y]:
            closest_core = -1
            closest_core_distance = 100000000
            for n in range(num_neighborhoods):
                core_distance = dist((x,y), neighborhoods[n]["core"])
                if core_distance < closest_core_distance:
                    closest_core = n
                    closest_core_distance = core_distance
                    neighborhoods[closest_core]["points"].append((x,y))

This code sucks lmao. The joys of prototyping! Sometimes you want to just get something working, so you build it the most absolutely smoothbrained way possible, knowing that the big-O of it is garbage, because you’re not even sure if you’re going to need it in a week, and leave optimizing ‘til later.

For all of this code, all this five-indent monstrosity is doing is iterating over every point in the map and, if it exists, checking which of the neighborhood cores it’s closest to and assigning that point to that neighborhood. That’s it! This is an absolutely hideous block of code to do that.⁵⁶

With that, every single space in the map is assigned to a neighborhood, and the map is properly divided. Here’s what that looks like on our example map.

With a count of three neighborhoods, we see our neighborhood 0 has set up a little enclave in the top right there, whereas neighborhoods 1 and 2 have split the rest of the island more of less straight down the middle. Neat!

What I Would Do Next If This Was A Workable Solution

So, with neighborhoods drawn out, the next step would be to split this map up and take advantage of the chunked nature we just created.

Probably what that looks like is the following steps:

1. Before we pull all of these neighborhoods apart from each other, make notes on where we want to draw transition points in them to move from one neighborhood to another (this is where that gates field on the neighborhoods object comes into play, you’d find points along the edge of each neighborhood to act as doorways, and mark them there, as well as noting what neighborhood was on the other side)

2. Create a single parent object called overworld or something to hold references to all of the maps

3. Create new map objects representing each of the neighborhoods in isolation, with the coordinates of each space relocalized to a new (0,0) placed at the top left of each neighborhood, rather than the entire map

4. Randomly populate each neighborhood with game stuff

5. Build the rest of the game to only load and display whatever neighborhood you’re currently in at a time

Why I’m Not Doing Any Of That And Actually Most Of This Codebase Is Going Into That Warehouse The Ark of The Covenant Gets Put In At The End of Raiders of the Lost Ark

Having rapidly built all of this stuff out in the course of two days in a beachside coffee shop in Port Townsend, I ultimately came to the conclusion that this is definitely not how I should be building my worldmap. Three main reasons:

1. This is admittedly a problem that could be aided with some algorithm reevaluation, but a lot of my approaches here scale like shit to a larger game world. I’ve been showing a 20x20 game map in my examples, and even on a 100x100 map it generates relatively quickly, but on anything large enough for the game I’m envisioning (like, 10,000x10,000), it starts to chug, which, like, of course it does, it has to process a hundred million spaces for some of these steps. Again, some optimization for things like sampling random edge spaces for deletion, or for calculating neighborhood membership, could remedy that, but I’m not gonna because..

2. This map doesn’t really look like a city does it? Not really. It’s always kind of a weird spindly blob thing that looks more like an island than a city, which is interesting, but not really what I’m going for. In fact, if we think about how cities are formed in real life, we might start to realize another sort of shape makes far more sense, because…

3. Neighborhoods in real American cities aren’t really centered on focal points that radiate outwards, they are instead usually defined as an assemblage of blocks: buildings or collections of buildings contrained by the four-ish streets that form their edges. The road network, not distance from an arbitrary point, creates the layout of neighborhoods.

A Revelation, and Next Steps

These thoughts in concert happened to lead to my next hypothesis for map generation. Note that game design doesn’t necessarily have to be strictly subservient to the nature of the real world: my city doesn’t necessarily have to be built in the same way that a real city is, because at the end of the day it isn’t built like a real city, it’s built by a nerd on a computer. However, adopting a process reminiscent of the way real cities and neighborhoods form could, I hypothesize, solve some of my problems.

Here’s the idea for the new revision: instead of chipping the world away from one big block, assemble it out of a bunch of tiny blocks, which are, in this case, literal city blocks: squareish chunks of world map bordered with road on all four sides which can be arranged in a 2-dimensional grid to assemble both a world map and a grid-system road network.

Instead of randomly chipping away at the edges, we can build ourselves a library of shapes for edge blocks, allowing our procedural generation to randomly select one of these templates based on where in the larger grid this particular edge lies (if it’s a corner, a middle edge, kind of a peninsula, stuff like that).

Neighborhood calculation becomes much easier, as we can now assign neighborhood membership to entire blocks rather than to individual spaces, meaning instead of having to calculate membership for NxN spaces, we only have to do it for MxM blocks, where M is the world size of the map N divided by the edge size of a block B (and likely to be in the 10s or 100s rather than the, you know, millions).

We also no longer have big walls dividing all of our neighborhoods, which is good for verisimilitude, because few cities after ‘91 have weird big walls with gated checkpoints dividing their neighborhoods. One big open world!

And then, looking even further beyond, we can engage with the block as the atomic unit of map design. We can draw roads within a single block, knowing that we always have a grid over the entire map to fall back on. We can then assign buildings to these roads and populate the world and the city by block, rather than just randomly scattering shit across blob-shaped neighborhoods.

So, I’m gonna go back to the lab and write this up. I’ll keep you posted with the results!

1. The effects of this double/triple/quadruple counting of hanging edge/corner points on the odds of said points being deleted diminish rapidly as the size of the game world increases. A playable game space for what I’m scoping for looks like a 10,000x10,000 square when it starts out at minimum, which means that starting deletion_candidates list starts with exactly 40,004 entries in it. 2/40,004 odds aren’t significantly better than 1/40,004 odds.

2. I actually only caught this bug just now! If the point chosen was one of our redundantly-represented corners from earlier, this will only delete one instance of it from our deletion_candidates list, meaning we might pick it again later and “waste” a deletion. Whoops!

3. Generally, assuming your programming language of choice lets you access list items by list index in constant time which, to my knowledge, most of them do

4. You math geniuses in the crowd might note that it’s not exactly N x N operations. Every time you grab a number out of the unsorted list and place it into its proper position, the size of the unsorted chunk of the list reduces by 1, so first you have to search through N numbers, then N-1, then N-2, and so on, until the very final number is the very last remaining number. We in the computer science world are what academics call “lazy” and “not gonna do all that fuckin’ math”, so it gets sorta rounded up to O(n^2). What we care about is the nature by which the speed scales to the size of the problem space, less so than the precise numbers.

5. The smart way to do this, probably, is to instead utilize breadth-first search again, starting with a subset of points (probably the neighborhood cores), and staking “claims” on all of their neighbors, each representing a point, a neighborhood core that is claiming it, and its distance to that core (starting at 0, as all of the cores are 0 away from themselves). Whenever you grab a claim out of the queue, if it’s a closer claim than the current one, you override the claimed point’s neighbor value, then queue up claims on all of its neighbors. There’s optimizations you could do, but the code probably ends up looking a little cleaner

6. Alternatively, I could just be smart and realize that I’m using the set of all points in the worldmap relatively frequently and that checking for that is a huge pain in the ass, so instead of iterating over the whole map and doing the “is it a point that exists” check over and over again, I should probably just, as soon as I’m done building the map, create a set that contains every valid point and then just iterate over that. Saves me three of the five indentations here.